Deep recurrent optical flow learning for particle image velocimetry data
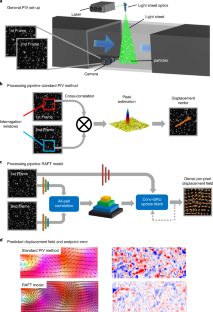
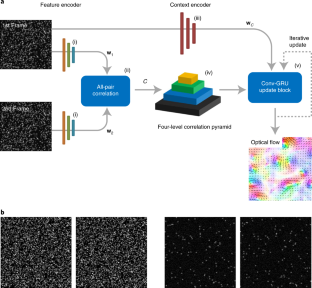
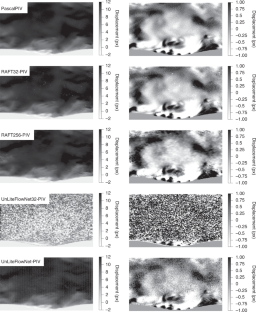
A wide range of problems in applied physics and engineering involve learning physical displacement fields from data. In this paper we propose a deep neural network-based approach for learning displacement fields in an end-to-end manner, focusing on the specific case of particle image velocimetry (PIV), a key approach in experimental fluid dynamics that is of crucial importance in diverse applications such as automotive, aerospace and biomedical engineering. The current state of the art in PIV data processing involves traditional handcrafted models that are subject to limitations including the substantial manual effort required and difficulties in generalizing across conditions. By contrast, the deep learning-based approach introduced in this paper, which is based on a recent optical flow learning architecture known as recurrent all-pairs field transforms, is general, largely automated and provides high spatial resolution. Extensive experiments, including benchmark examples where true gold standards are available for comparison, demonstrate that the proposed approach achieves state-of-the-art accuracy and generalization to new data, relative to both classical approaches and previously proposed optical flow learning schemes.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
133,45 € per year
only 11,12 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
Recurrent graph optimal transport for learning 3D flow motion in particle tracking
Article 04 May 2023

Bubble velocimetry using the conventional and CNN-based optical flow algorithms
Article Open access 13 July 2022
Identifying key differences between linear stochastic estimation and neural networks for fluid flow regressions
Article Open access 08 March 2022
Data availability
The public PIV particle image database (Problem Class I) can be found at https://github.com/shengzesnail/PIV_dataset. The Problem Class 2 dataset can be downloaded from Zenodo (https://doi.org/10.5281/zenodo.4432496) 56 .
Code availability
A reference implementation of RAFT can be found at https://github.com/princeton-vl/RAFT. A Code Ocean compute capsule, which contains a pre-built compute environment and the source code, is available at https://codeocean.com/capsule/7226151/tree/v1 (https://doi.org/10.24433/CO.4413978.v1) 57 .
References
- Braun, M., Schröder, W. & Klaas, M. High-speed tomographic PIV measurements in a DISI engine. Exp. Fluids60, 146 (2019). ArticleGoogle Scholar
- Stella, A., Guj, G., Kompenhans, J., Raffel, M. & Richard, H. Application of particle image velocimetry to combusting flows: design considerations and uncertainty assessment. Exp. Fluids30, 167–180 (2001). ArticleGoogle Scholar
- Pielhop, K., Schmidt, C., Zholtovski, S., Klaas, M. & Schröder, W. Experimental investigation of the fluid–structure interaction in an elastic 180 curved vessel at laminar oscillating flow. Exp. Fluids55, 1816 (2014). ArticleGoogle Scholar
- Saaid, H. et al. In vitro volumetric lagrangian particle tracking and 4D pressure field in a left ventricle model. In Summer Biomechanics, Bioengineering and Biotransport Conference (SB3C, 2019).
- Li, W. et al. Analysis of a drag reduced flat plate turbulent boundary layer via uniform momentum zones. Aerospace Sci. Technol.96, 105552 (2020). ArticleGoogle Scholar
- Herbst, S. L., Kähler, C. J. & Hain, R. Sd7003 airfoil in large-scale free stream turbulence. In 35th AIAA Applied Aerodynamics Conference 3748 (AIAA, 2017).
- Nobach, H. & Honkanen, M. Two-dimensional gaussian regression for sub-pixel displacement estimation in particle image velocimetry or particle position estimation in particle tracking velocimetry. Exp. Fluids38, 511–515 (2005). ArticleGoogle Scholar
- Scarano, F. & Riethmuller, M. L. Iterative multigrid approach in PIV image processing with discrete window offset. Exp. Fluids26, 513–523 (1999). ArticleGoogle Scholar
- Westerweel, J. & Scarano, F. Universal outlier detection for PIV data. Exp. Fluids39, 1096–1100 (2005). ArticleGoogle Scholar
- Karri, S., Charonko, J. & Vlachos, P. P. Robust wall gradient estimation using radial basis functions and proper orthogonal decomposition (POD) for particle image velocimetry (PIV) measured fields. Measurement Sci. Technol.20, 045401 (2009). ArticleGoogle Scholar
- Teed, Z. & Deng, J. RAFT: recurrent all-pairs field transforms for optical flow. In European Conference on Computer Vision 402–419 (Springer, 2020).
- Dosovitskiy, A. et al. Flownet: learning optical flow with convolutional networks. In Proc. IEEE International Conference on Computer Vision 2758–2766 (IEEE, 2015).
- Ilg, E. et al. Flownet 2.0: evolution of optical flow estimation with deep networks. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 2462–2470 (2017).
- Hui, T.-W., Tang, X. & Change Loy, C. Liteflownet: a lightweight convolutional neural network for optical flow estimation. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 8981–8989 (IEEE, 2018).
- Sun, D., Yang, X., Liu, M.-Y. & Kautz, J. PWC-Net: CNNs for optical flow using pyramid, warping, and cost volume. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 8934–8943 (IEEE, 2018).
- Hur, J. & Roth, S. Iterative residual refinement for joint optical flow and occlusion estimation. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 5754–5763 (IEEE, 2019).
- Yang, G. & Ramanan, D. Volumetric correspondence networks for optical flow. In Advances in Neural Information Processing Systems 794–805 (NIPS, 2019).
- Rabault, J., Kolaas, J. & Jensen, A. Performing particle image velocimetry using artificial neural networks: a proof-of-concept. Meas. Sci. Technol.28, 125301 (2017). ArticleGoogle Scholar
- Lee, Y., Yang, H. & Yin, Z. PIV-DCNN: cascaded deep convolutional neural networks for particle image velocimetry. Exp. Fluids58, 171 (2017). ArticleGoogle Scholar
- Cai, S., Liang, J., Gao, Q., Xu, C. & Wei, R. Particle image velocimetry based on a deep learning motion estimator. IEEE Trans. Instrum. Meas.69, 3538–3554 (2019). ArticleGoogle Scholar
- Cai, S., Zhou, S., Xu, C. & Gao, Q. Dense motion estimation of particle images via a convolutional neural network. Exp. Fluids60, 73 (2019). ArticleGoogle Scholar
- Lagemann, C., Lagemann, K., Schröder, W. & Klaas, M. Deep artificial neural network architectures in PIV applications. In 13th International Symposium on Particle Image Velocimetry (ISPIV, 2019).
- Horn, B. K. & Schunck, B. G. Determining optical flow. In Techniques and Applications of Image Understanding Vol. 281, 319–331 (1981).
- Bruhn, A., Weickert, J. & Schnörr, C. Lucas/Kanade meets Horn/Schunck: combining local and global optic flow methods. Int. J. Comput. Vision61, 211–231 (2005). ArticleGoogle Scholar
- Mayer, N. et al. What makes good synthetic training data for learning disparity and optical flow estimation? Int. J. Comput. Vision126, 942–960 (2018). ArticleGoogle Scholar
- Perry, B. A. & Mueller, M. E. Joint probability density function models for multiscalar turbulent mixing. Combust. Flame193, 344–362 (2018). ArticleGoogle Scholar
- Zhang, C., Duan, L. & Choudhari, M. M. Direct numerical simulation database for supersonic and hypersonic turbulent boundary layers. AIAA J.56, 4297–4311 (2018). ArticleGoogle Scholar
- Schlatter, P. et al. Turbulent boundary layers up to Reθ = 2500 studied through simulation and experiment. Phys. Fluids21, 051702 (2009). ArticleGoogle Scholar
- Zhang, M. & Piggott, M. D. Unsupervised learning of particle image velocimetry. In International Conference on High Performance Computing 102–115 (Springer, 2020).
- Huang, H., Fiedler, H. & Wang, J. Limitation and improvement of PIV. Exp. Fluids15, 263–273 (1993). ArticleGoogle Scholar
- Soria, J., Cater, J. & Kostas, J. High resolution multigrid cross-correlation digital PIV measurements of a turbulent starting jet using half frame image shift film recording. Optics Laser Technol.31, 3–12 (1999). ArticleGoogle Scholar
- Zaki, T. A. From streaks to spots and on to turbulence: exploring the dynamics of boundary layer transition. Flow Turbul. Combust.91, 451–473 (2013). ArticleGoogle Scholar
- Li, Y. et al. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul.91, N31 (2008). ArticleGoogle Scholar
- Perlman, E., Burns, R., Li, Y. & Meneveau, C. Data exploration of turbulence simulations using a database cluster. In Proc. 2007 ACM/IEEE Conference on Supercomputing 1–11 (IEEE, 2007).
- Albers, M. et al. Drag reduction and energy saving by spanwise traveling transversal surface waves for flat plate flow. Flow Turbul. Combust.105, 1–33 (2020).
- Jonschkowski, R. et al. What matters in unsupervised optical flow. In European Conference on Computer Vision 557–572 (Springer, 2020).
- Rubbert, A., Albers, M. & Schröder, W. Streamline segment statistics propagation in inhomogeneous turbulence. Phys. Rev. Fluids4, 034605 (2019). ArticleGoogle Scholar
- Charonko, J. J. & Vlachos, P. P. Estimation of uncertainty bounds for individual particle image velocimetry measurements from cross-correlation peak ratio. Meas. Sci. Technol.24, 065301 (2013). ArticleGoogle Scholar
- Xue, Z., Charonko, J. J. & Vlachos, P. P. Particle image velocimetry correlation signal-to-noise ratio metrics and measurement uncertainty quantification. Meas. Sci.Technol.25, 115301 (2014). ArticleGoogle Scholar
- Michaelis, D., Neal, D. R. & Wieneke, B. Peak-locking reduction for particle image velocimetry. Meas. Sci. Technol.27, 104005 (2016). ArticleGoogle Scholar
- Cai, S. et al. Artificial intelligence velocimetry and microaneurysm-on-a-chip for three-dimensional analysis of blood flow in physiology and disease. Proc. Natl Acad. Sci. USA118, e2100697118 (2021). ArticleGoogle Scholar
- Blundell, C., Cornebise, J., Kavukcuoglu, K. & Wierstra, D. Weight uncertainty in neural network. In Proc. 32nd International Conference on Machine Learning Vol. 37, 1613–1622 (ICML, 2015).
- Morrell, M. C., Hickmann, K. & Wilson, B. Particle image velocimetry analysis with simultaneous uncertainty quantification using bayesian neural networks. Measurement Science and Technology (2021).
- Siam, M., Valipour, S., Jagersand, M. & Ray, N. Convolutional gated recurrent networks for video segmentation. In 2017 IEEE International Conference on Image Processing 3090–3094 (IEEE, 2017).
- Paszke, A. et al. Automatic differentiation in pytorch. In 31st Conference on Neural Information Processing Systems (NIPS 2017).
- Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2014).
- Marquardt, P., Klaas, M. & Schröder, W. Experimental investigation of isoenergetic film-cooling flows with shock interaction. AIAA J.57, 3910–3923 (2019). ArticleGoogle Scholar
- Astarita, T. & Cardone, G. Analysis of interpolation schemes for image deformation methods in PIV. Exp. Fluids38, 233–243 (2005). ArticleGoogle Scholar
- Gallivan, K., Grimme, G. & Van Dooren, P. A rational Lanczos algorithm for model reduction. Numer. Algorithms12, 33–63 (1996). ArticleMathSciNetGoogle Scholar
- Schrijer, F. & Scarano, F. Effect of predictor–corrector filtering on the stability and spatial resolution of iterative PIV interrogation. Exp. Fluids45, 927–941 (2008). ArticleGoogle Scholar
- Raffel, M. et al. Particle Image Velocimetry: A Practical Guide (Springer, 2018).
- Héas, P., Mémin, E., Heitz, D. & Mininni, P. D. Power laws and inverse motion modelling: application to turbulence measurements from satellite images. Tellus A64, 10962 (2012). ArticleGoogle Scholar
- Lee, M. & Moser, R. D. Direct numerical simulation of turbulent channel flow up to Reτ ≈ 5200. J. Fluid Mech.774, 395–415 (2015). ArticleGoogle Scholar
- Resseguier, V., Mémin, E. & Chapron, B. Geophysical flows under location uncertainty. Part II. Quasi-geostrophy and efficient ensemble spreading. Geophys. Astrophys. Fluid Dyn.111, 177–208 (2017). ArticleMathSciNetGoogle Scholar
- Scharnowski, S. & Kähler, C. J. On the loss-of-correlation due to PIV image noise. Exp. Fluids57, 1–12 (2016). ArticleGoogle Scholar
- Lagemann, C., Lagemann, K., Mukherjee, S. & Schröder, W. Dataset—Deep Recurrent Optical Flow Learning for Particle Image Velocimetry Data (Zenodo, 2021).
- Lagemann, C., Lagemann, K., Mukherjee, S. & Schröder, W. Recurrent All-Pairs Field Transforms for Particle Image Velocimetry Data (CodeOcean, 2021).
Acknowledgements
We thank P. Marquardt for his support and many fruitful discussions, M. Albers for providing DNS data and M. Klaas for proofreading parts of the manuscript. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputers HAWK at Höchstleistungsrechenzentrum Stuttgart (www.hlrs.de) and Juwels at the Forschungszentrum Jülich (www.fz-juelich.de).
Author information
Authors and Affiliations
- Institute of Aerodynamics Aachen, RWTH Aachen University, Aachen, Germany Christian Lagemann & Wolfgang Schröder
- Statistics and Machine Learning, DZNE, Bonn, Germany Kai Lagemann & Sach Mukherjee
- University of Cambridge, Cambridge, UK Sach Mukherjee
- JARA Center for Simulation and Data Science, RWTH Aachen University, Aachen, Germany Wolfgang Schröder
- Christian Lagemann









